El triángulo rectángulo es un polígono de 3 lados, que se caracteriza por tener un ángulo recto de 90˚ y otros dos ángulos (α y β), que se denominan ángulos menores y la suma de ambos ángulos es de 90˚:

α + β = 90˚

El triángulo rectángulo está compuesto por 3 elementos: 2 catetos que son los lados contiguos al ángulo recto: lado “a” y  lado “b”, y la hipotenusa que es el lado mayor y esta opuesto al ángulo recto, lo llamaremos “c”.

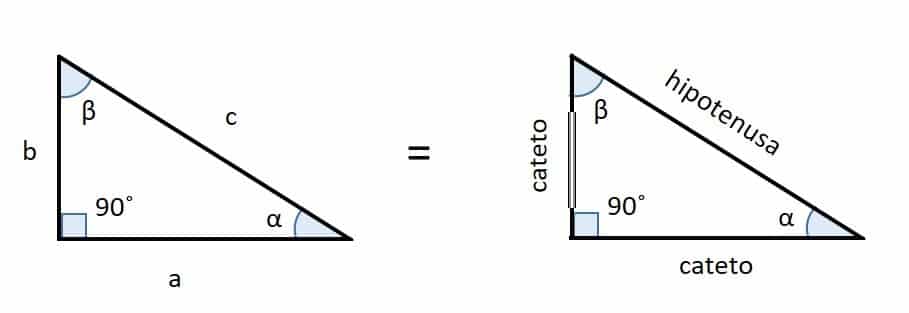
La altura del triángulo es el lado «b» y la base del triángulo es el lado «a».

Tipos de Triangulo rectángulo.

Existen dos tipos de triángulos rectángulos, ambos mantienen su característica básica de un ángulo recto de 90˚. A continuación te explicamos su diferencia:

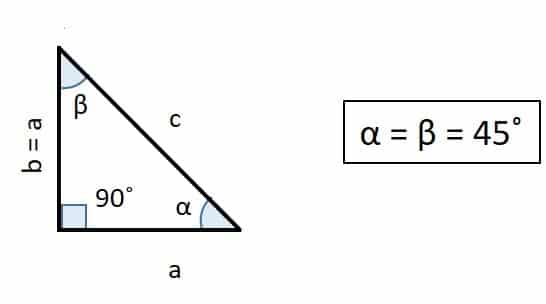
1.Triangulo rectángulo Isósceles: Cuando tanto α como β son 45˚. Por lo tanto el lado “a” es igual a lado “b”. Entonces

• α = β = 45˚

• Lado a (base) = lado b (altura) = a

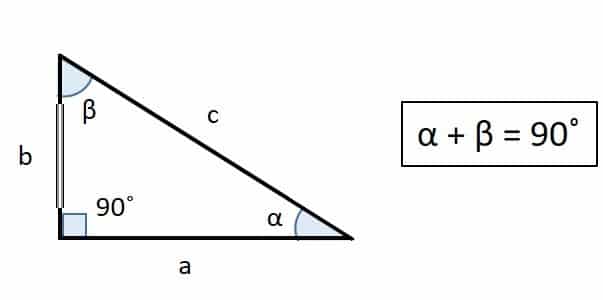
2.Triangulo rectángulo escaleno: cuando todos los ángulos del triángulo son diferentes y por lo tanto cada lado es diferente. El ángulo recto sigue siendo 90 ˚

Sacar la altura de un triángulo con el Teorema de Pitágoras

El teorema de Pitágoras, es la relación matemática de los 3 lados del triángulo rectángulo. Esta fórmula indica que la hipotenusa al cuadrado es igual al cateto 1 al cuadrado más el cateto 2 al cuadrado:

c² = a² + b²

Por lo tanto si conocemos cuanto miden dos lados de un triángulo rectángulo, podremos saber cuánto mide el tercer lado con la fórmula del Teorema de Pitágoras.

Ejemplo: Calcular la Hipotenusa con Pitágoras.

Para calcular la hipotenusa con Pitágoras, debemos conocer tanto la medida del lado “a” (base), como la medida del lado “b” (altura) y con esta información usamos la fórmula para sacar la altura un triangulo (valor de «C»)

c² = a² + b²

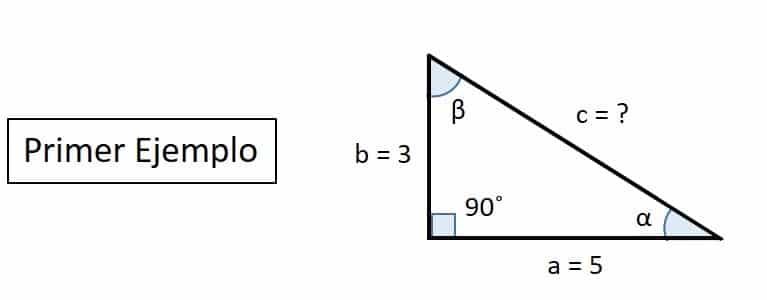
Pasos para calcular la hipotenusa de un triángulo rectángulo cuando conocemos cuanto mide su base “a” y cuanto su altura “b”

• Paso 1: despejar la “c” en la fórmula del Teorema de Pitágoras. Como esta elevado al cuadrado, pasa al otro lado como raíz cuadrada:

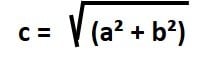
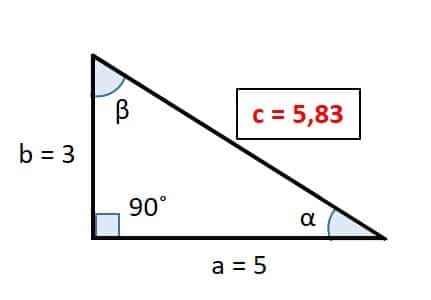
• Paso 2: sustituimos los valores conocidos en la formula a = 5 y b = 3

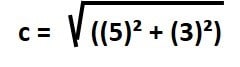
• Paso 3: cogemos la calculadora y vamos resolviendo la operación matemática paso a paso para evitar equivocarnos:
  • (5)² = 5 * 5 = 25
  • (3)² = 3 * 3 = 9

• 25 + 9 = 34

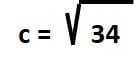
• La raíz cuadrada de 34 = 5,83

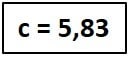
Es así como, usando el teorema de Pitágoras hemos calculado que para un triángulo de base 5 cm y altura 3 cm, su hipotenusa es de 5,83cm

Ejemplo: sacar la altura con Pitágoras.

En nuestro segundo ejercicio conocemos la medida de la base del triángulo “a” y la medida de la hipotenusa “c” y queremos conocer ¿Cuánto tiene de altura “b” del triángulo rectángulo?

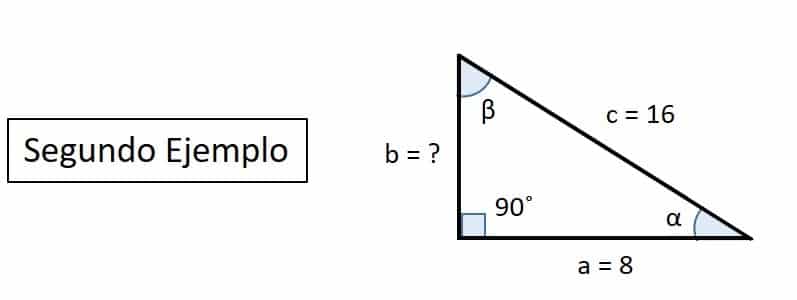
Pasos para calcular la altura de un triángulo rectángulo con base e hipotenusa conocida:

• Paso 1: debemos despejar la “b” de la fórmula del teorema de Pitágoras:

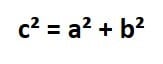
Como el término a² está sumando pasa al otro lado restando:

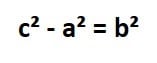
El cuadrado de la b pasa al otro lado como raíz cuadrada:

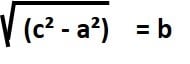
• Paso 2: Sustituimos los valores numéricos: a = 8 y c = 16. Entonces:

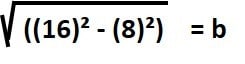
• Paso 3: resolvemos cada operación con una calculadora y vamos escribiendo los resultados para evitar equivocarnos: 
  • (16)² = 16 * 16 = 256
  • (8) ² = 8 * 8 = 64

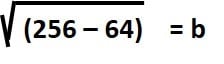
• 256 – 64 = 192

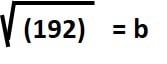
• Raíz de 192 = 13,86

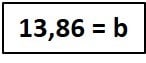
Listo, la respuesta es que para un triángulo rectángulo  de base 8 cm e hipotenusa de 16 cm, su altura es de 13,86cm.

Cómo sacar la Altura de un Triángulo Rectángulo conociendo el Área

Recordemos que el área de un triángulo se calcula con la siguiente formula: base por altura entre 2.

Con esta fórmula, si tenemos el área y la medida de la base del triángulo rectángulo “a”, podemos saber cuánto es la altura “b” de nuestro triangulo.

Ejemplo: Calcula la Altura con el Área.

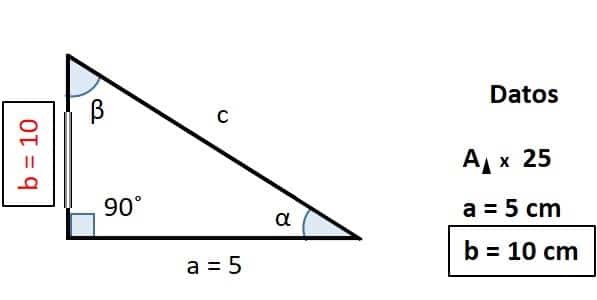
Con los siguientes datos, calcular ¿Cuál es la altura del triángulo rectángulo?

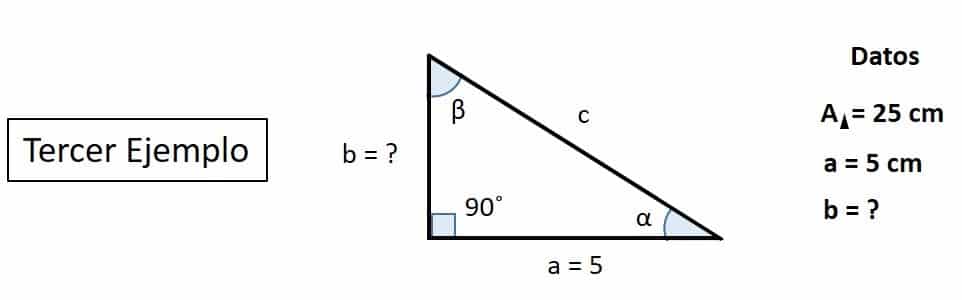
Pasos para sacar la altura de un triángulo rectángulo conociendo su área y cuanto mide la base:

Paso 1: de la fórmula del área del triángulo, despejar la altura “b”:

• Como el 2 está dividiendo, pasa multiplicando:

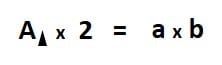
• Como la base “a” está multiplicando, pasa dividiendo:

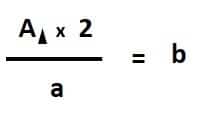
• Paso 2: sustituimos en la formula los valores conocidos: área del triángulo = 25 y a=5

• Paso 3: resolvemos la operación matemática:
  • 25 * 2 = 50
  • 50 / 5 = 10

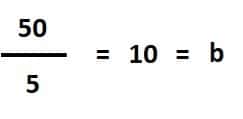
Listo, entonces hemos calculado la altura del triángulo rectángulo, que es 10 cm, cuando su base mide 5 cm y su área es de 25 cm

Con estos ejemplos esperamos hayas entendido como calcular la altura de un triángulo rectángulo, tanto con el teorema de Pitágoras como con la fórmula del área del triángulo.

De igual forma si tienes alguna duda, déjanos tus comentarios.