Si estas interesado en conocer el procedimiento metódico para resolver cualquier suma de fracciones, este es el post correcto. Te enseñaremos paso a paso como resolver una suma de fracciones de manera ordenada y metódica.
En este artículo, primero te enseñaremos como realizar sumas de fracciones con el mismo denominador, luego sumas de fracción con diferente denominador y, por último, haremos algunos ejercicios de suma de fracción con respuestas, para que practiquemos juntos.
Tabla de Contenidos
Sumar fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, la operación es muy sencilla. Detallamos el procedimiento a continuación:
- Paso 1: escribir el denominador común.
- Paso 2: sumar algebraicamente los numeradores
Ejemplo 1:

Ejemplo 2:
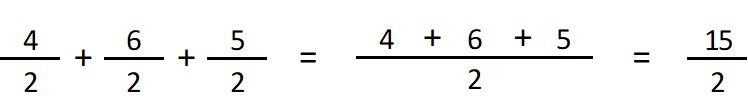
Como se observa en los ejemplos sumar dos o más fracciones con un mismo denominador, es una operación de dos pasos.
Sumar Fracciones con denominador diferente
Realmente para sumas fracciones, es necesario que tengan un denominador común. Por esta razón para sumar fracciones con diferentes denominadores, hallaremos un denominador común mediante el método del mínimo común múltiplo
Este procedimiento es un poco más largo, pero también es sencillo. Y aquí, te lo explicaremos de forma metódica y simple a través de un ejemplo práctico.
Pasos para sumar fracciones con diferente denominador mediante el uso de un ejemplo práctico:
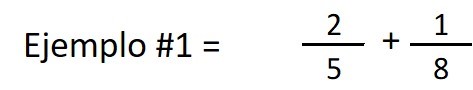
- Paso 1: Calcular el m.c.m. entre los denominadores. En nuestro ejemplo, calcular el m.c.m (5, 8) = 40

- Paso 2: escribir una raya larga con el m.c.m como denominador común:
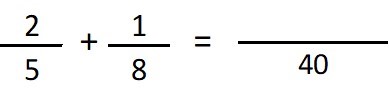
- Paso 3: vamos a dividir el denominador común (40) entre el denominador de la primera fracción (5) y luego, el resultado (8), lo vamos a multiplicar por el numerador de esa misma fracción (2) y vamos a escribir el resultado (16) sobre la línea larga que acabamos de hacer:
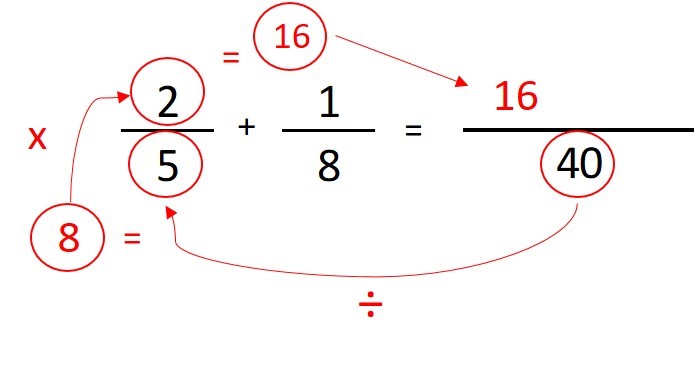
- Paso 4: escribimos el símbolo matemático que este entre ambas fracciones sobre la línea, después del numero hallado en el paso 3:
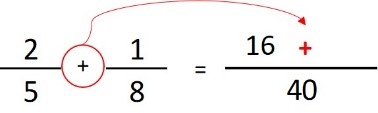
- Paso 5: Repetimos la operación del paso 3. Pero con la siguiente fracción. Dividimos el denominador común (40) entre el denominador de la segunda fracción (8),y el resultado (5), lo multiplicamos por el numerador (1). El resultado lo anotamos sobre la raya después del símbolo matemático (+):
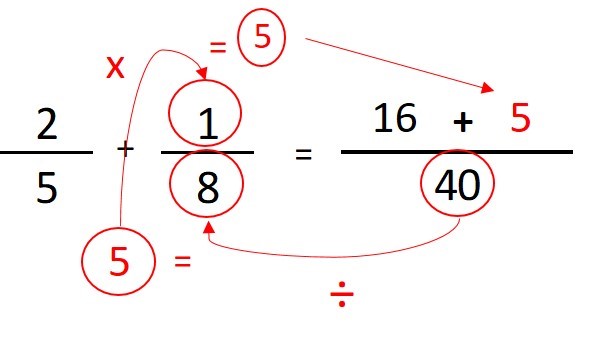
- Paso 6: sumamos algebraicamente los dos numeradores.

Observamos como de forma metódica y simple se puede resolver una suma de fracciones con diferente denominador. Siendo el resultado final de nuestro ejemplo 21/40.
Ejercicios prácticos resueltos
Para practicar un poco lo aprendido, realizaremos a continuación un conjunto de ejercicios de sumar fracciones con respuestas para que practiquemos juntos.
Ejercicio 1
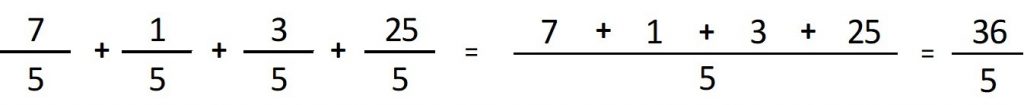
Suma de fracción con mismo denominador: primero escribimos el denominador común y luego sumamos algebraicamente los numeradores. Respuesta (36/5)
Ejercicio 2
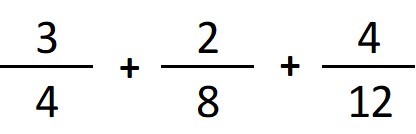
- Paso 1: hallamos el m.c.m. de los denominadores:
- 4 = 2²
- 8 = 2³
- 12 = 2³ x 3
m.c.m. (4, 8, 12) = 2³ x 3 = 8 x 3 = 24
– Paso 2: Hacemos la raya grande con el m.c.m (24) como denominador común:
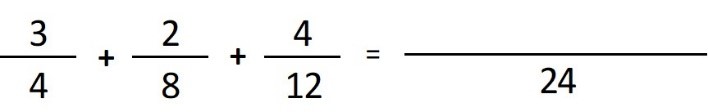
- Paso 3: dividimos el denominador común (24) entre el denominador de la primera fracción (4) y el resultado (6), lo multiplicamos por el numerador de la primera fracción (3), y el resultado (18) lo escribimos sobre la línea junto con el símbolo matemático (+) que le sigue:
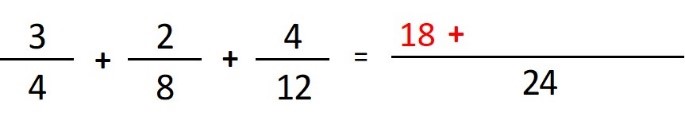
- Paso 4: dividimos el denominador común (24) entre el denominador de la segunda fracción (8) y el resultado (3), lo multiplicamos por el numerador de la segunda fracción (2), y el resultado (6) lo escribimos sobre la línea junto con el símbolo matemático (+) que le sigue:
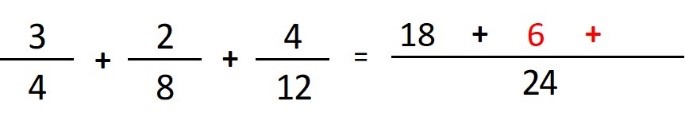
- Paso 5: dividimos el denominador común (24) entre el denominador de la tercera fracción (12) y el resultado (2), lo multiplicamos por el numerador de la tercera fracción (4), y el resultado (8) lo escribimos sobre la línea larga:
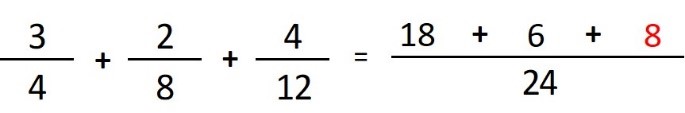
- Paso 6: Sumamos algebraicamente los numeradores (18 + 6 + 8 = 32) y escribimos el denominador común (24) y obtenemos el resultado final:

Esperamos haberlos ayuda a sumar con fracciones, cualquier duda puede dejar un comentario y con gusto te explicaremos
