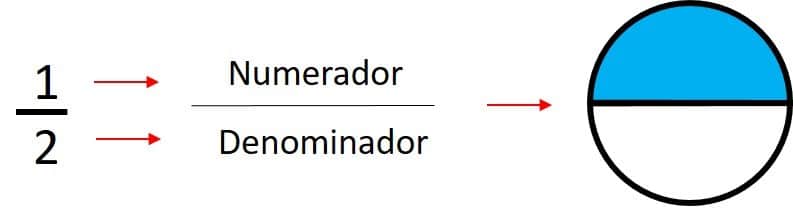
El denominador de una fracción representa el número de partes iguales en que dividiremos un todo y el numerador representa cuantas de esas partes quiero coger. Por ejemplo si yo tengo una pizza y la pico en dos partes iguales y me como una de esas partes, esto se vería expresado con la siguiente fracción:
Las fracciones se pueden amplificar y simplificar para crear nuevas fracciones equivalentes a las anteriores. En este artículo te enseñaremos: que es una fracción equivalente, como se amplifican fracciones y como se simplifican fracciones. Como siempre trabajaremos con ejemplos para ir practicando lo aprendido.
Lee esto -> Como se clasifican las matrices
Tabla de Contenidos
Qué son Fracciones Equivalentes.
Dos fracciones son equivalentes cuando representan la misma parte. Es decir, cuando tienen el mismo valor decimal.
Por ejemplo: si compramos una pizza, veamos estos tres posibles casos:
- La picas en 2 pedazos y te comes uno de los pedazos
- La picas en 4 pedazos y te comes 2 pedazos
- La picas en 8 pedazos y te comes 4 pedazos
En cualquiera de los casos te estas comiendo media pizza, vamos a verlo gráficamente:
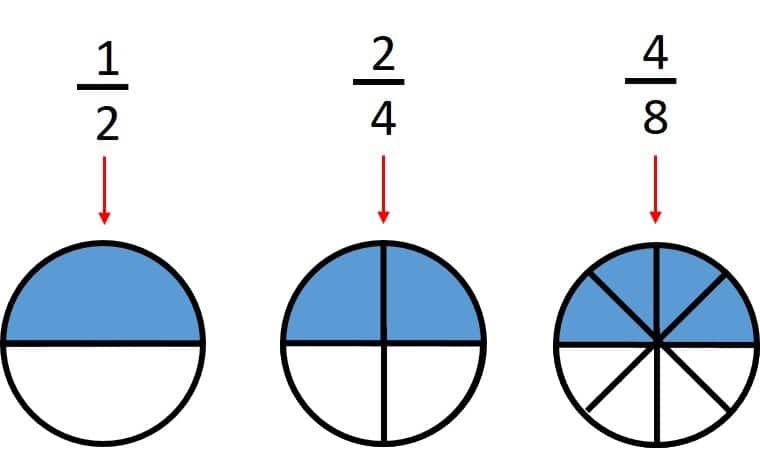
Observando como todas las fracciones son equivalentes, ya que todas representan la misma parte: media pizza.
¿Cómo saber si dos fracciones son equivalentes matemáticamente? Debes calcular el valor decimal de cada fracción y debe ser el mismo. El valor decimal de una fracción se calcula dividiendo el numerador entre el denominador. Practiquemos con las mismas fracciones de arriba:
- Valor decimal de 1/2 = 1 entre 2 = 0,5
- Valor decimal de 2/4 = 2 entre 4 = 0,5
- Valor decimal de 4/8 = 4 entre 8 = 0,5
Comprobando entonces que nuestras tres fracciones son equivalentes, entonces ¿Cómo se amplifican y simplifican fracciones?
Te puede interesar -> Divisiones con decimales
Cómo Amplificar Fracciones
Amplificar una fracción, significa calcular una fracción equivalente de numerador y denominador mayor a la fracción original.
Para amplificar una fracción debes multiplicar el numerador y el denominador por el mismo número.
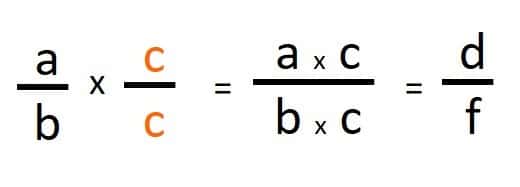
Ejemplos de amplificar una fracción:
- Amplificar la fracción 3/5
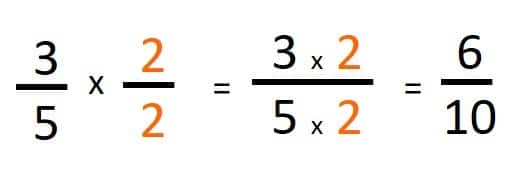
Para amplificar la fracción multiplicamos tanto el numerador como el denominador por 2, obteniendo que 3/5 y 6/10 son fracciones equivalentes.
Pero la pudimos amplificar por 3, por 4, por 5, etc., por el número que nosotros queramos siempre y cuando multipliquemos el numerador y el denominador por el mismo número:
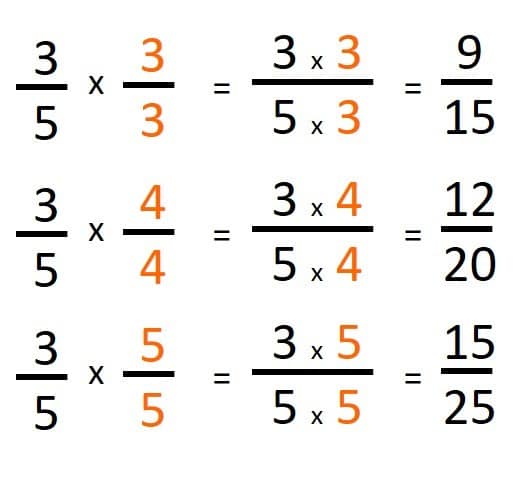
Con este proceso hemos calculado varias fracciones equivalentes a nuestra fracción original: 3/5, utilizando el método de amplificación de fracciones. ¿Te parece si comprobamos que todas las fracciones que calculamos son equivalentes?
Para esto calculamos el valor decimal de cada resultado dividendo el numerador entre el denominador:
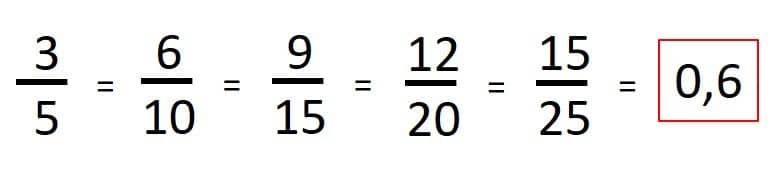
Comprobando así, que al amplificar una fracción original, calculas una fracción equivalente de numerador y denominador mayor a la fracción original.
Lee esto -> Como sacar la altura de un triangulo
Cómo Simplificar Fracciones.
Para simplificar fracciones debemos dividir el numerador y el denominador por el mismo número, para hallar una fracción equivalente con numerador y denominador menor a la fracción original.
Una fracción solo se puede simplificar si tanto el numerador como el denominador son divisibles por el mismo número.
Una fracción se puede simplificar hasta llegar a la fracción irreductible, que es cuando ya no existe una fracción equivalente de menor numerador y denominador.
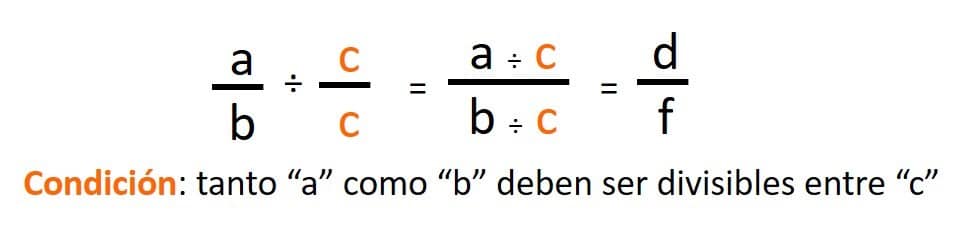
Reglas para Simplificar Fracciones
Hay 3 reglas muy importantes que nos pueden ayudar a simplificar fracciones. Estas reglas sirven para saber entre que numero son divisibles tanto el numerador como el denominador:
- Si tanto el numerador como el denominador terminan en número par, entonces la fracción es divisible entre 2:

- Si sumo los dígitos que componen el número del numerador y hago lo mismo con el denominador, y ambos resultados son múltiplos de 3. Entonces la fracción es divisible entre 3:

- Si tanto el numerador como el denominador terminan en 0 y/o 5, entonces la fracción es divisible entre 5:

Conociendo estas 3 reglas, podremos hallar el divisor común de manera más sencilla y rápida.
Ejemplos de Simplificación de Fracciones:
- Simplificar la Fracción 120/40 hasta su mínima expresión (hasta que sea irreductible)
- Evaluamos numerador y denominador, y vemos que ambos terminan en 0, por lo tanto son divisibles entre 5, simplificamos entre 5:
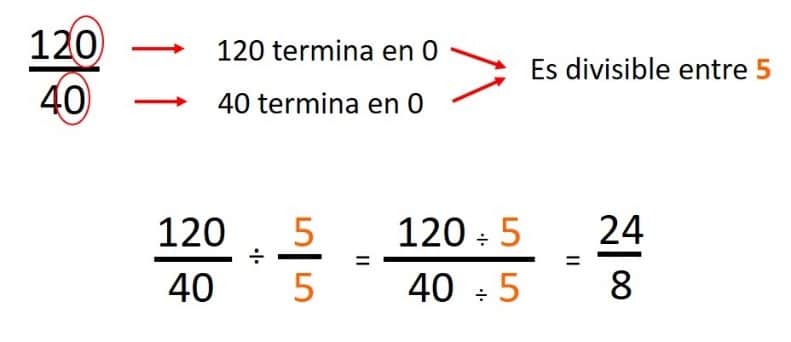
- Nos preguntamos: ¿el resultado: 24/8 aún se puede seguir simplificando? Comprobamos y vemos que ambos terminan en número par, por lo tanto son divisibles entre 2:
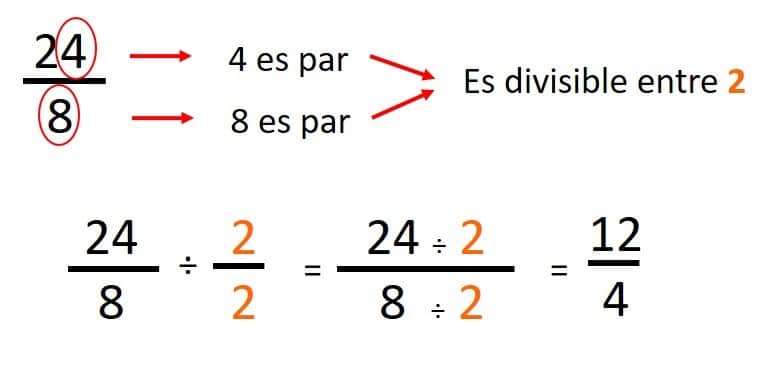
- Nos preguntamos: ¿el resultado: 12/4 aún se puede seguir simplificando? Comprobamos y vemos que ambos terminan en número par, por lo tanto son divisibles entre 2:
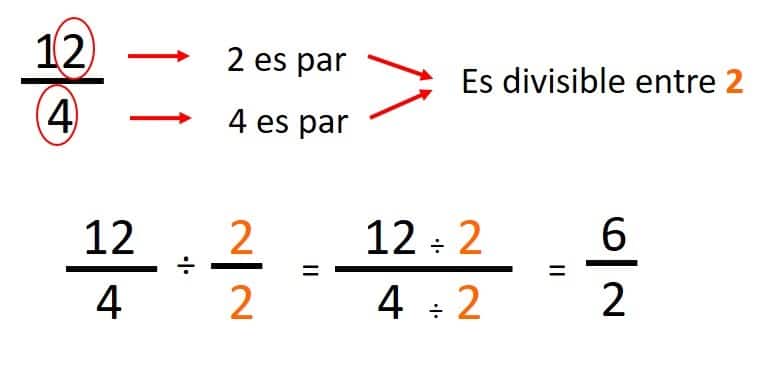
- Nos preguntamos: ¿el resultado: 6/2 aún se puede seguir simplificando? Comprobamos y vemos que ambos terminan en número par, por lo tanto son divisibles entre 2:
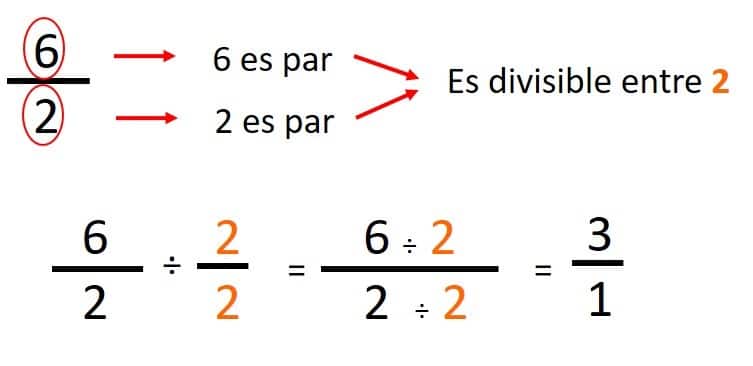
- Nos preguntamos: ¿el resultado: 3/1 aún se puede seguir simplificando? Comprobamos y nos damos cuenta que ya no es simplificable, porque 3/1 es igual a 3. Y ya no hay forma de conseguir una fracción equivalente de menor numerador y denominador.
Hemos calculado que la mínima expresión de 120/40 = 3/1 = 3. Y hemos calculado esto a través de la simplificación de fracciones, encontrando las fracciones equivalentes de menor numerador y denominador.
Esperamos que ahora sepas como amplificar y simplificar fracciones. De igual manera, si tienes alguna duda, déjanos tus comentarios.
